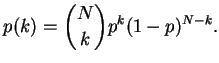Next: Problem solved with a
Up: Throwing N stones into
Previous: Throwing N stones into
Contents
Firstly, we focus on one box only:
For each thrown stone, the probability that a stones falls in this particular
box is
 . The probability that
it falls on another box is
. The probability that
it falls on another box is
 .
.

Figure 4:
Probability tree leads to a binomial distribution.
If we throw 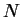 stones, we can build a binary tree of height
stones, we can build a binary tree of height 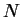 . In each
tree's node, we choose the left path if the stone falls into the particular box we focus. The right path
is chosen if it falls in another one. The probability that no stone falls in
our box after
. In each
tree's node, we choose the left path if the stone falls into the particular box we focus. The right path
is chosen if it falls in another one. The probability that no stone falls in
our box after 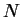 throws is
throws is
 and follows the rightmost
arm of the tree with height
and follows the rightmost
arm of the tree with height 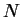 .
.
In general, the probability to have  stones into one box follows the
binomial distribution. With
stones into one box follows the
binomial distribution. With
 , we state
In N binomial k, we select all paths in the tree with
, we state
In N binomial k, we select all paths in the tree with  stones inside the box and
we assign to each sub path the correct probability depending if it was a success
or a failure.
In short, we have a
stones inside the box and
we assign to each sub path the correct probability depending if it was a success
or a failure.
In short, we have a  probability distribution for each box of our
problem where
probability distribution for each box of our
problem where  and
and
 .
. ![$ E[B(n,p)]$](img24.png) is
is
 .
.

Figure 5:
Dependence versus independence
To compute the standard deviation, one can choose a Poisson distribution as
approximation for  . This is because
. This is because 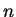 is big (
is big (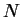 ) and
) and  is small (
is small (
 ). For the Poisson distribution,
). For the Poisson distribution, 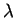 is
then
is
then
 . The variance of the Poisson distribution is
. The variance of the Poisson distribution is
 , The
standard deviation for Poisson is therefore
, The
standard deviation for Poisson is therefore
 . Alternatively, one can compute
. Alternatively, one can compute  for
for
 using
using
 and a differentiation trick. For large
and a differentiation trick. For large
 s, standard deviation and variance are the same for both distributions,
s, standard deviation and variance are the same for both distributions,
 for Binomial and
for Binomial and
 for Poisson.
for Poisson.
Here, it is important to notice the following: while
 is the probability that one particular box is
empty, it is not possible to generalize with
is the probability that one particular box is
empty, it is not possible to generalize with
 to the problem
where all boxes have at least one stone; the boxes are not independent from
each other: a stone that does not land into a box does not fall apart but
lands in another box, as in Figure 5.
to the problem
where all boxes have at least one stone; the boxes are not independent from
each other: a stone that does not land into a box does not fall apart but
lands in another box, as in Figure 5.




Next: Problem solved with a
Up: Throwing N stones into
Previous: Throwing N stones into
Contents
Tiziano Mengotti
2004-03-27
![]() . The probability that
it falls on another box is
. The probability that
it falls on another box is
![]() .
.

![]() stones, we can build a binary tree of height
stones, we can build a binary tree of height ![]() . In each
tree's node, we choose the left path if the stone falls into the particular box we focus. The right path
is chosen if it falls in another one. The probability that no stone falls in
our box after
. In each
tree's node, we choose the left path if the stone falls into the particular box we focus. The right path
is chosen if it falls in another one. The probability that no stone falls in
our box after ![]() throws is
throws is
![]() and follows the rightmost
arm of the tree with height
and follows the rightmost
arm of the tree with height ![]() .
.