



Next: How to implement a
Up: Example: Feynman Kac plugin
Previous: Seed management
Contents
This plugin solves Exercise 2.2 of the "Introduction to Parallel Computing"
book described at page 82 [1].
We solve a partial differential equation inside an elliptical region by Monte
Carlo simulations of the Feynman-Kac formula. The following partial
differential equation is defined in a three-dimensional ellipsoid E:
where the ellipsoidal domain is
The potential is
Our Dirichlet boundary condition is
 when
when

The goal is to solve this boundary value problem at
 by a
Monte Carlo simulation. At the heart of the simulation lies the Feynman-Kac
formula, which in our case (
by a
Monte Carlo simulation. At the heart of the simulation lies the Feynman-Kac
formula, which in our case (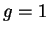 ) is
) is
which describes the solution  in terms of an expectation value of a
stochastic process
in terms of an expectation value of a
stochastic process  whose initial value
whose initial value  . Here
. Here
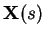 is a Brownian motion starting
from
is a Brownian motion starting
from
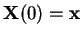 and
and  is its exit time from
is its exit time from 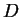 .
.
It is important to point out that the
 operator in simulation
means
operator in simulation
means
 for samples of size
for samples of size 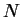 .
.
The plugin pde3d.dll can be called in two different ways:
0,[a],[b],[c],feynmankac3d
1,[a],[b],[c],[initialx],[initialy],[initialz],feynmankac3d
The first call passes the ellipses axes as parameter. The function
feynmankac3d stored in pde3d.dll generates first randomly
a point
 inside the ellipse.
In the second call, we can specify the initial
inside the ellipse.
In the second call, we can specify the initial
0 or 1 inform the plugin on how many parameters are loaded on the stack.
From this initial interior point
 we integrate
the following system of stochastic differential equations (
we integrate
the following system of stochastic differential equations (
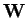 is a
Brownian motion). We use
is a
Brownian motion). We use 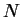 realizations of
realizations of
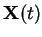 to integrate.
to integrate.
For each realization, we integrate this set of equations until
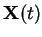 exits at time
exits at time
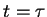 using the trapezoidal rule [1]. Finally, we compute
using the trapezoidal rule [1]. Finally, we compute
 to get the solution.
to get the solution.
To plot the error, we compare it to the exact analytical solution of the partial
differential equation, computed by two differentiations:
The error in the plugin's graphical output is plotted as an oscillating green
line around the y axis. After oscillating for a while, the error tends to
converge to the y axis. Only one out of many random walks (
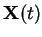 ) is
plotted with red or white colors.
) is
plotted with red or white colors.
Roughly speaking, we free a horde of random walkers from an initial
point. These walkers diffuse while  is integrated with rate
is integrated with rate
 on the potential
on the potential 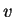 until they
reach the boundary of the ellipse. All walks are averaged in a similar way as
it is done with the pi plugin to get the function value at the chosen
initial point. The diffusion process of the walkers,
distributed as a trivariate normal density, weights points near the initial
point more than points far away.
until they
reach the boundary of the ellipse. All walks are averaged in a similar way as
it is done with the pi plugin to get the function value at the chosen
initial point. The diffusion process of the walkers,
distributed as a trivariate normal density, weights points near the initial
point more than points far away.
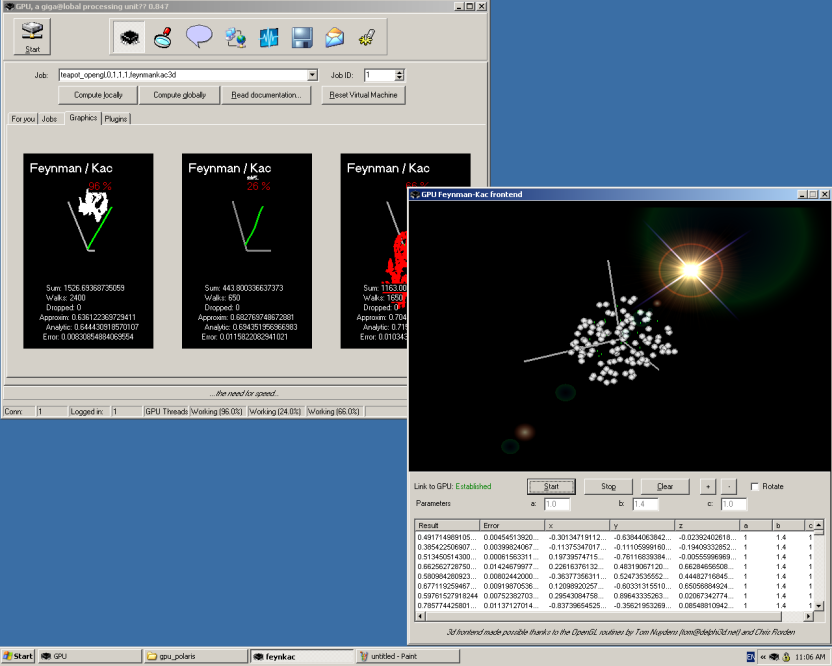
Figure 13:
GPU computing the Feynman-Kac problem and corresponding frontend.




Next: How to implement a
Up: Example: Feynman Kac plugin
Previous: Seed management
Contents
Tiziano Mengotti
2004-03-27
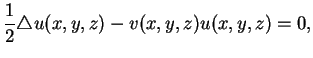
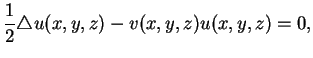
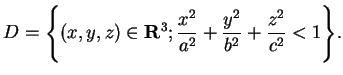



![]() operator in simulation
means
operator in simulation
means
![]() for samples of size
for samples of size ![]() .
.
![]() inside the ellipse.
In the second call, we can specify the initial
inside the ellipse.
In the second call, we can specify the initial
![]() we integrate
the following system of stochastic differential equations (
we integrate
the following system of stochastic differential equations (
![]() is a
Brownian motion). We use
is a
Brownian motion). We use ![]() realizations of
realizations of
![]() to integrate.
to integrate.

