



Next: Approximation with a Poisson
Up: Problem from a different
Previous: Problem from a different
Contents
The probability
 of the realization of at least one among the events
of the realization of at least one among the events
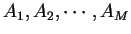 is given by an alternating sum
Hence, the the probability that all cells are occupied is
This probability is the solution to the recurrence formula that gave the
number of arrangements with no cells empty divided by the total number of
arrangements
is given by an alternating sum
Hence, the the probability that all cells are occupied is
This probability is the solution to the recurrence formula that gave the
number of arrangements with no cells empty divided by the total number of
arrangements 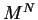 .
.
Tiziano Mengotti
2004-03-27
