Problem from a different perspective

We follow [28] here. We first change the way we look at the problem; we imagine now to have the $N$ stones in a line, and to assign to each of them a number between $1$ and $M$ - this number is the box the stone falls in. There are $M^{N}$ possible distributions, each with probability $\frac{1}{M^{N}}=M^{-N}$. We seek the probability $p_{0}(N,M)$ of finding all cells occupied.

Let $A_{k}$ be the event that cell number $k$ is empty ( $k=1,2,\cdots,n$). In this situation all $N$ stones are placed in the remaining $(M-1)$ cells, and this can be done in $(M-1)^{N}$ different ways. Similarly, there are $(M-2)^N$ arrangements, leaving two preassigned cells empty, etc. Accordingly and with $\frac{(M-1)^N}{M^N}=(1-\frac{1}{M})^N$:

$$p_{i}=(1-\frac{1}{M})^{N}, p_{ij}=(1-\frac{2}{M})^{N}, p_{ijk}=(1-\frac{3}{M})^{N}, \cdots$$

and hence for every $1 \leq \nu \leq M$

$$S_{\nu}=\binom{M}{\nu}(1-\frac{\nu}{M})^{N}.$$

$S_{\nu}$ is the sum of probabilities, where each arrangement with $\nu$ cells empty appears once and only once.

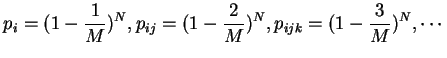
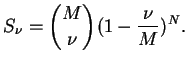
We use now an important theorem proved in [28, pg 99]: