Simulation with a plugin

Using the plugin stattest.dll, we estimate our problem with a simulation.

We computed for each point in the graph the N stones to M boxes problem $100000$ times. Each time, we looked if we were able to cover the domain M with at least one stone and we averaged to get the $p_{!0}(N,M)$ probability.

Syntax for the plugin is:

[M],[N],[number of attempts],throwNstonestoMboxes

The plugin gives two probabilities back:

[probability that all cells are occupied],
[1-(average coverage probability)]

The first probability is $p_{0}(N,M)$. The numbers fit our formula and the approximation with $e^{-\lambda}$.

Figure 7: Probability $p_{0}(N,M)$ to cover entire domain with at least one stone

In the second probability, we looked at what percentage of the domain was not covered with at least one stone through all $100000$ realizations of the experiment. The graphs shows that the uncovered domain decreases independently from the size $M$ of our problem, in respect to $\frac{N}{M}$.

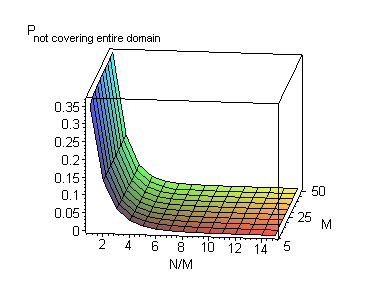
Figure 8: Average failure probability in respect to coverage