Throwing N stones into M boxes

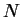We reformulate the problem in the previous section differently: assuming we have $M$ boxes, how many stones $N$ do we have to throw randomly to get at least one stone inside each box with probability $p_{0}$ provided that $N \geq M$?

Notice that in the reformulation, beside the constraint were we ensure that the number of stones is at least equal to the number of boxes, we introduced a probability $p_{0}$. This because it is impossible to ensure that at least one stone will be in each box with 100% probability. Although with very little probability, all stones might fall in the same box even if we threw thousands of them. Therefore, we can think only in expectation values. 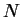In particular, we are interested if the number of stones to be thrown $N$ grows with the sub domain size $M$ while keeping a reasonable and constant probability $p_{0}$.

The problem is often referred in literature as the "coupon collector problem" or "classical occupancy problem"[28]. A nice Java applet to visualize it is [27].