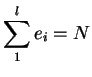Reducing the problem to a 2D-volumetric argument

Given a random subgraph $G_{sub}(n \subseteq N, e \subseteq E)$ of $G(N,E)$. How many edges connect $G_{sub}$ to $G \setminus G_{sub}$? We imagine $G_{sub}$ and $G$ really big graphs embedded in the plane; imagine coloring red nodes belonging to $G_{sub}$ and yellow for nodes in $G \setminus G_{sub}$. Now we look at them from far away: nodes and edges look like a tiny lattice and eventually disappear into two uniform areas, one red and one yellow. Assume we set $n = A \propto r^2$ where $A$ is a graph's area. The perimeter of the graph's area is then proportional to $r$, and the number of outgoing connections proportional to $r \propto \sqrt{n}$, too.

It is important to note here that the form of the subgraph changes area up to a constant ( $A_{1}=\pi r^2$ for a circle and $A_{2}=4 r^2$ for a square) but does not change the radius dimensionality.

Figure 10: $G_{sub}$ and $G$ seen from far away

Assume we could solve the problem stated in this paragraph: we could then sum up $e_{i}$ until we reach $N$. In the analogic mechanism, $e_{i}$ is the number of nodes added to each level of the tree to the bin.

$$\sum_{1}^{l}{e_{i}} = N$$

with $e_{i}$: number of outgoing edges for graph with $i$ nodes and $l$ maximum path length.