



Next: Applying the formula
Up: Small world problem estimated
Previous: Reducing the problem to
Contents
If we decide that our lattice is not constrained to planes, then we propose the
following nodes with constant degree  as building blocks.
as building blocks.

Figure 11:
Building blocks, lattice where we embed  and
and  .
.
We chose building blocks so that they generate homogeneous grids and with fixed
length edges. Both constraints are necessary for the volumetric argument we want to use. Homogeneity is similar
to the requirement for planar graphs in normal graph theory that edges do not
cross. Edge-crossing would generate inhomogeneities with fixed length edges on
2D grids.
If  is even, we naturally choose edges perpendicular to each other. Two
counter-directed edges of the building block form an independent axis in the
is even, we naturally choose edges perpendicular to each other. Two
counter-directed edges of the building block form an independent axis in the
 dimensional axis. Therefore, we set
If
dimensional axis. Therefore, we set
If  is odd, we might looked puzzled at the fractional dimension, a sort
of in between dimension.
is odd, we might looked puzzled at the fractional dimension, a sort
of in between dimension.
Furthermore, we know that the boundary of a subgraph has a dimension less (for
a sphere
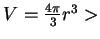 , but
, but
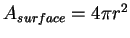 ). In general, if the
subgraph is
). In general, if the
subgraph is  -dimensional, the volume is proportional to
-dimensional, the volume is proportional to 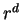 and the
boundary to
and the
boundary to 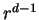 .
Size of the random subgraph
.
Size of the random subgraph 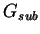 with
with 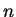 nodes is then:
The number of outgoing edges is proportional to the size of the boundary,
nodes is then:
The number of outgoing edges is proportional to the size of the boundary,
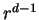 namely.
namely.
We now start in the middle of our subgraph, and we subsequently add nodes
until we reach the boundary. In the analogous mechanism of adding nodes means putting
them into the bin, 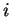 , representing the height of the tree and the boundary is
reached until all nodes are into the bin.
We imagine a tiny lattice of nodes and we therefore turn summation into an integral:
Thus:
and:
Solving for
, representing the height of the tree and the boundary is
reached until all nodes are into the bin.
We imagine a tiny lattice of nodes and we therefore turn summation into an integral:
Thus:
and:
Solving for 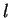 gives:
Solving for
gives:
Solving for  requires a numerical approximation.
requires a numerical approximation.
Resuming, we consider 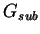 embedded in
embedded in 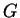 , both in a homogeneous
, both in a homogeneous
 -dimensional grid
composed by myriads of the above mentioned building blocks. We let
-dimensional grid
composed by myriads of the above mentioned building blocks. We let 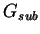 grow until it reaches the same size of
grow until it reaches the same size of 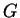 through summation and we infer
through summation and we infer 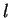 .
.
Results are very similar to the Mandelbrot's formula
that relates mass (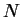 ) and linear extension
) and linear extension 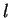 with the exponent
with the exponent  [25].
[25].




Next: Applying the formula
Up: Small world problem estimated
Previous: Reducing the problem to
Contents
Tiziano Mengotti
2004-03-27

![]() and
and ![]() .
.

![]() and
and ![]() .
.
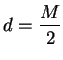
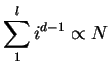
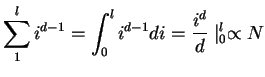
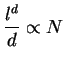
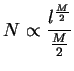
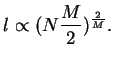
![]() embedded in
embedded in ![]() , both in a homogeneous
, both in a homogeneous
![]() -dimensional grid
composed by myriads of the above mentioned building blocks. We let
-dimensional grid
composed by myriads of the above mentioned building blocks. We let ![]() grow until it reaches the same size of
grow until it reaches the same size of ![]() through summation and we infer
through summation and we infer ![]() .
.