Let ![]() be the number of arrangements leaving none of the
be the number of arrangements leaving none of the ![]() bins
empty [28]. We imagine adding an additional bin. This bin contains k stones
(
bins
empty [28]. We imagine adding an additional bin. This bin contains k stones
(
![]() ) but not 0, so that we can express the number of arrangements
in the other bins with
) but not 0, so that we can express the number of arrangements
in the other bins with ![]() . Therefore, the number of arrangements
leaving none of the
. Therefore, the number of arrangements
leaving none of the ![]() bins empty satisfies a recurrence,
bins empty satisfies a recurrence,
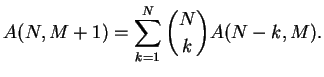

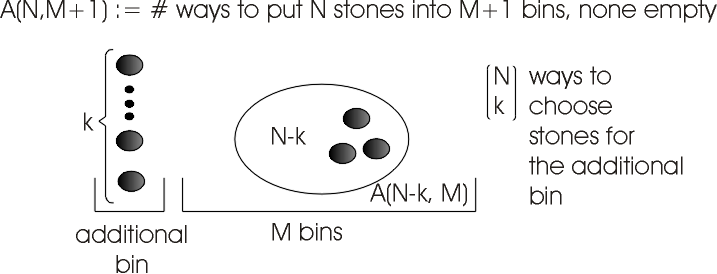
Figure 6: Composing the recurrence formula